Homogeneity puzzles

Why results about homogeneous neural networks can apply to some non-homogeneous ones

An intriguing footnote, from Merrill et al. (2023)

More intrigue, this time from Haim et al. (2022)

As I’ve written about before, the question of why neural networks can generalise is a bit of a mystery. In short, it seems like there’s too much expressivity and too little data for classical learning theory to predict that the learnt model will handle new inputs well. So it there must be some serendipity, with neural network training having properties making it disposed (implicitly biased) to learning the types of functions we want to learn.

This implicit bias is pretty hard to study in full generality. For one, neural networks aren’t a standard thing. There is a multitude of architectures and training setups. So results will often zoom in on a specific simplified setting to understand its dynamics better. This post takes a look at one such simplifying assumption, namely homogeneity, and investigates why results about homogeneous neural networks puzzlingly appear to hold even for some non-homogeneous ones. This seems like a potentially-important-to-understand oddity, because basically all neural networks used in practice are non-homogeneous.

Homogeneity

By homogeneous neural networks, we mean architectures where the mapping from points in parameter space to the function implemented is a homogeneous function. Intuitively, this means that scaling up the parameters doesn’t change the behaviour of the model (but could change the scale of the outputs).

A formal definition, from Nacson et al. (2019); think of g as the map from parameter space to the function that the parameters implement

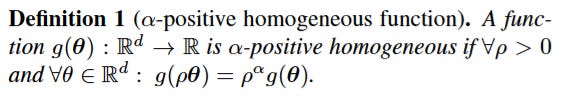
Vanilla neural networks with ReLU activation and biases are not homogeneous, but without biases they are homogeneous.

Results about homogeneous nets

Next, let’s take a look at some of results that have been shown to hold for homogeneous neural networks.

Sphere-projected training

An implication of homogeneity is that you can train by projecting onto a parameter-space sphere after each optimisation step because the projection doesn’t change the direction of the parameter vector (which is what determines which function is implemented, up to scale). Another way to think about this is that homogeneity means that only the tangential direction of the training trajectory matters and not the radial component. The picture below shows what I mean by radial and tangential:

Margin-maximisation

There are results about the growth of the margin when homogeneous neural networks are trained on classification tasks (see these papers). Margin, loosely speaking, is about how decisively the neural network predicts the correct class. I’ve written more about margin-maximisation, and how it might relate to good generalisation.

Dataset reconstruction

Haim et al. (2022) show how to reconstruct some of the training examples from the weights of a homogeneous neural network trained to classify images:

Some reconstructed images, from figure 1 in their paper

The core insight that enables their reconstruction is that we know that the final trained parameter values will approximately be a maximum-margin direction for the dataset. So we can optimise a randomly-initialised candidate dataset until it satisfies this condition with respect to the parameters.

The puzzle

All of the results outlined in the previous sections have been empirically observed to continue holding even when the architecture is changed to include biases! As far as I can tell, there is no great account of why this might be the case.

The plot below shows sphere-project gradient descent working equally well for homogeneous and non-homogeneous networks:

The network is a simple feedforward network, trained on MNIST. It seems like whether or not there are biases (i.e., whether or not homogeneity is present) it is fine to throw away all information about the scale of the weights by projecting onto the sphere with radius 20.

Margins are empirically observed to grow during training even when there are biases:

From Lyu and Li (2020)

And reconstruction of training data is possible with biases too!

The first row shows reconstructions from the weights of a trained non-homogeneous neural network, and the second row shows the corresponding original training image - from figure 11 of Haim et al. (2022)

When there are biases, it’s unclear why any of these results continue holding. Yet we can still train pretty well even when we throw away all of the information about the scale of the weights by projecting onto a sphere! So what’s going on here?

A solution?

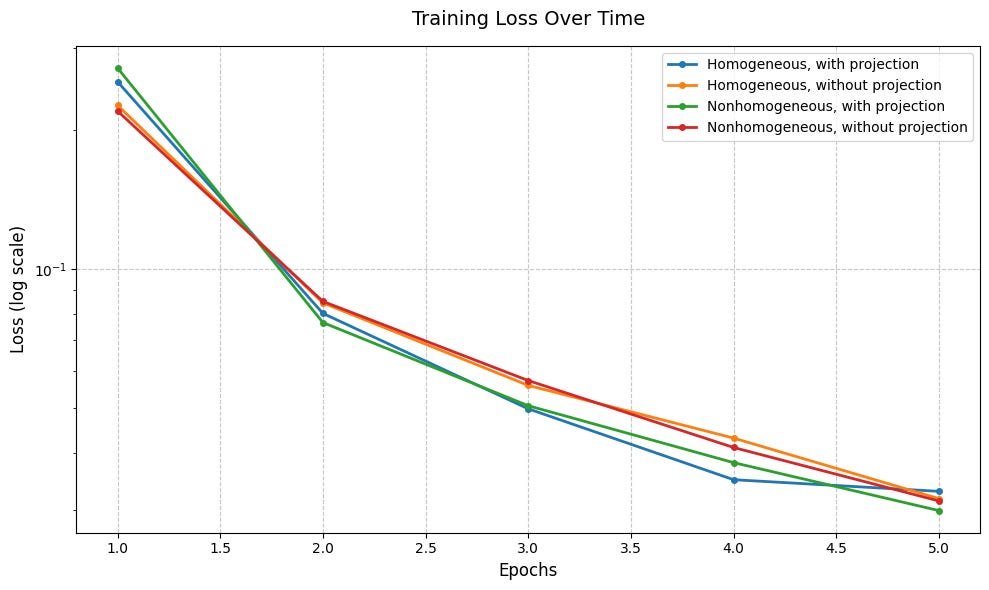
Well, a key observation is that this sphere-projected gradient descent doesn’t work in the case when you set the radius of the sphere too small. What I think is going on here is that when you scale up the weights linearly, the scale of the activations in later layers scales up superlinearly. So the biases are small compared to the activations and the network is approximately homogeneous. I’m not super satisfied with this though.

I test this, and the explanation seems at least partially correct! Above a certain scale, increasing the magnitude of the network’s parameters maintains performance.

How scaling up or down the parameters of a trained non-homogeneous network affects classification accuracy

But does enough norm growth occur during training to make the results about the behaviour of homogeneous neural networks relevant? This paper’s results suggests that the answer might be yes!

An aside: weight decay

Weight decay adds a term to loss functions that encourages the norm of the weights to be small. Why might this be beneficial?

Weight decay provides another minor piece of evidence that the behaviour of homogeneous neural network training might be similar to the non-homogeneous case. Homogeneous neural networks give a nice intuition about why weight decay might improve generalisation - they make the gradients point more in the tangential direction (as the radial direction is the direction that grows the weights’ norms, and weight decay penalises growing norm). So this means that the loss’s reduction is due to a meaningful change in network behaviour and not just growing the output to achieve lower loss and thus “locking in” current behaviour.

But weight decay works well for non-homogeneous networks too! To me, this suggests that a similar dynamic might be occurring, with radial growth of weights being associated to loss reduction due to increasing scale rather than loss reduction due to changed behaviour. Which in turn would suggest that there are similarities in the parameterisation geometry between homogeneous neural networks and ones, where changing along the radial direction keeps behaviour similar. This is isn’t super strong evidence of course; maybe weight decay has other benefits apart from pushing update directions into the tangential direction. And maybe this won’t apply to more sophisticated attention-based architectures where norm growth is useful for other reasons (such as increasing sparsity).